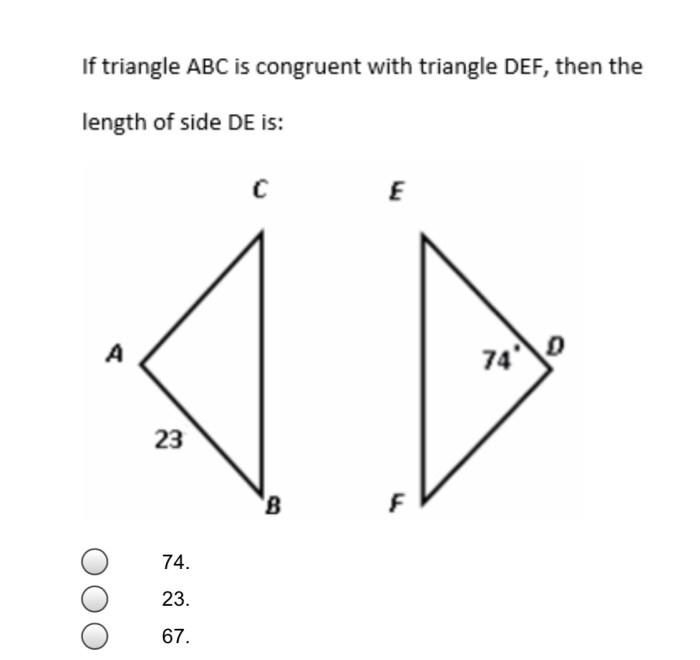
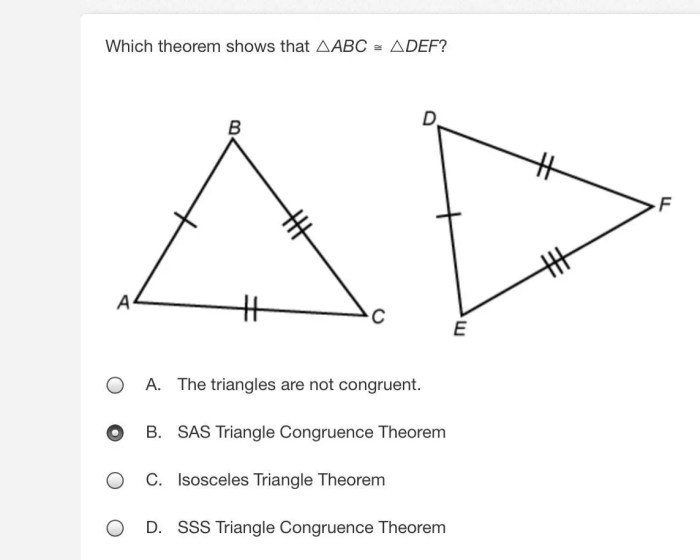
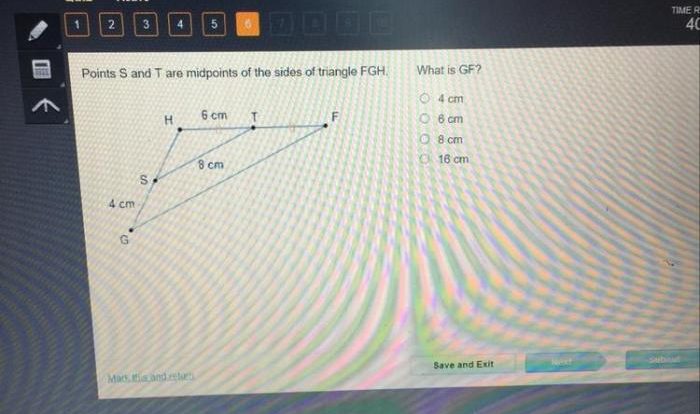
What is a correct congruence statement for the triangles shown? Congruence statements establish the equality of triangles based on specific criteria, enabling us to analyze and compare their properties. This discussion will explore the concept of congruence statements, examine different criteria, and determine the appropriate congruence statement for given triangles.
Congruence statements provide a foundation for geometric proofs and applications in fields like architecture and engineering. Understanding these statements empowers individuals to make accurate deductions and solve problems involving triangles.
Congruence Statements for Triangles
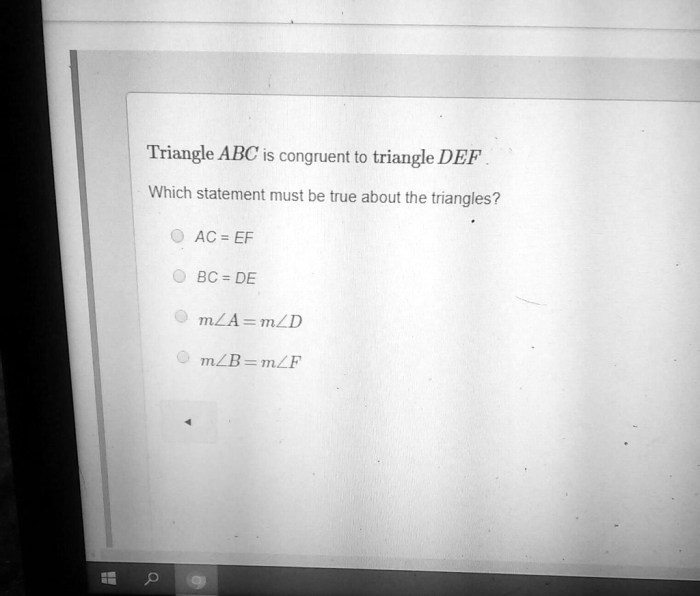
Congruence statements for triangles describe the conditions under which two triangles are considered to be identical in size and shape. These statements play a fundamental role in geometry and are essential for understanding the properties of triangles.
Congruence statements are based on the concept of congruence, which refers to the equality of two geometric figures. For triangles, congruence means that the corresponding sides and angles of the triangles are equal.
Congruence Criteria
There are several criteria that can be used to establish congruence between triangles. These criteria are based on the properties of the triangles and the relationships between their sides and angles.
- Side-Side-Side (SSS) Congruence: If the three sides of one triangle are equal to the corresponding three sides of another triangle, then the triangles are congruent.
- Side-Angle-Side (SAS) Congruence: If two sides and the included angle of one triangle are equal to the corresponding two sides and included angle of another triangle, then the triangles are congruent.
- Angle-Side-Angle (ASA) Congruence: If two angles and the included side of one triangle are equal to the corresponding two angles and included side of another triangle, then the triangles are congruent.
- Angle-Angle-Side (AAS) Congruence: If two angles and a non-included side of one triangle are equal to the corresponding two angles and non-included side of another triangle, then the triangles are congruent.
Congruence Statements for the Given Triangles, What is a correct congruence statement for the triangles shown
To determine the appropriate congruence statement for the given triangles, we need to examine their corresponding sides and angles.
Let’s consider two triangles, ΔABC and ΔDEF, where:
- AB = DE
- BC = EF
- AC = DF
- ∠A = ∠D
- ∠B = ∠E
- ∠C = ∠F
Since all three sides and all three angles of ΔABC are equal to the corresponding sides and angles of ΔDEF, we can conclude that the triangles are congruent by the Side-Side-Side (SSS) Congruencecriterion.
Proof of Congruence
To prove the congruence of ΔABC and ΔDEF using the SSS Congruence criterion, we need to demonstrate that the three sides of one triangle are equal to the corresponding three sides of the other triangle.
- Given: AB = DE, BC = EF, AC = DF
- By the definition of congruence, if two triangles have all three sides equal, then the triangles are congruent.
- Therefore, ΔABC ≅ ΔDEF.
Applications of Congruence Statements
Congruence statements have numerous applications in various fields, including geometry, architecture, and engineering.
- Geometry: Congruence statements are used to prove the properties of triangles and other geometric figures.
- Architecture: Congruence is essential for designing symmetrical structures and ensuring the accuracy of building plans.
- Engineering: Congruence is used in the design and construction of bridges, airplanes, and other structures where precise measurements and alignments are critical.
FAQ Explained: What Is A Correct Congruence Statement For The Triangles Shown
What is the SSS congruence criterion?
The SSS (Side-Side-Side) congruence criterion states that if the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent.
What is the SAS congruence criterion?
The SAS (Side-Angle-Side) congruence criterion states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
What is the ASA congruence criterion?
The ASA (Angle-Side-Angle) congruence criterion states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.